Math and Movement: A Poi Spinners Journey
 Fire poi 4 petal antispin flower vs extension
Fire poi 4 petal antispin flower vs extension As a circus flow artist, I spin many different types of props as a form of moving meditation. The ability to dance freely and meditatively with a prop is often referred to as 'Flow'. To be in flow is "being completely involved in an activity for its own sake. The ego falls away. Time flies. Every action, movement, and thought follows inevitably from the previous one, like playing jazz. Your whole being is involved, and you're using your skills to the utmost. We experience a loss of self-consciousness and a sense of complete mastery of the performance." (Csikszentmihalyi, 1993)
Flow Artists learn specific prop manipulation tricks, and then string these tricks into a sequence by using transitions. Smooth transitions between tricks can make for flawless dancing- to give the illusion of effortless flow.
There is another stream of circus arts that often operates in conjunction with flow, called Tech. Tech is a more mathematical focus on tricks, not only to have seamless transitions between movements of the body, but more focus on the attempt to create specific and deliberate patterns of light around the body with the prop. Tech spinners are usually less dynamic in their performance, but the patterns created by tech spinners are often 'clean' - more clearly visible than with a flow artist.
So, how does this apply to Math? For the purpose of this paper I will use Poi for an example. "The art of poi may be one of the most unique confluences of art, movement, math, and science in the modern era. At its root, the art is based in tribal dances practiced by the Maori of New Zealand for an unknown period before being exported to the Western world to integrate with a variety of martial arts, dance, and other prop manipulation styles. In its current form, spinning poi focuses on the creation of curves in space using a weighted end connected via a flexible tether to the performer’s hand." (Drexler, 3)
Poi was the prop that began my circus practice. I learned a few basic tricks, some transitions, and then moved on to learning other props. My practice the past year has brought me back to poi, but this time with a talented teacher, Kat. He has been not only teaching me new patterns and transitions, but the math theory behind the movements, and I am understanding math and patterns in exciting new ways. "Students truly “get” math when they see it applied in real-life ways they care about—in other words, when they see math as a tool they need and want.” (Wills, 8)
A mathematical understanding of motion in the art form allows practitioners to explore patterns in different ways. If we have a system, we can extrapolate from it. Many beautiful poi spinning patterns have been derived from the analysis of possible motions.
Having a classification system also means having a standard naming system; the sheer number of possible patterns is overwhelming. As such, communication with each other about the art can be impossible unless we are visually able to show the pattern we are referring too. "As much of the movement vocabulary for poi has been created on an ad-hoc basis or passed down via oral tradition rather than recorded or formalized in deliberate fashion, there exist strong regional differences in definitions, movement vocabularies, and interpretations of how movements interrelate to the point that such conflicts are all but inevitable." (Drexler, 4)
A mathematical system also allows us to teach ourselves how the pattern works, and to perfect its execution. For example, if the math says this pattern should have 4 loops in it of equal spacing apart, then why doesn't mine have them equally spaced apart? I must Practice more!
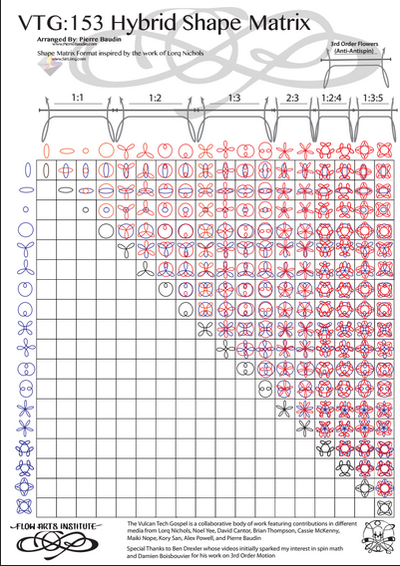
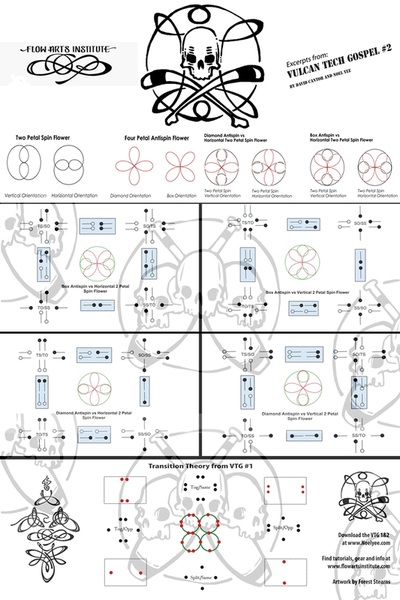
The most popular classification system for poi patterns is known as the Vulcan Tech Gospel, developed by Noel Yee. The VTG is focused on how two objects move in relation to each other, and provides diagrams of movement patterns along with a nomenclature of both movement, direction and rotation. It is “a treatise on technical prop manipulation that seeks to explain the entirety of sets of technique, using a predetermined set of constants and variables, in order to document the resulting patterns as well as provide tools for learning and understanding” (Cantor 2)
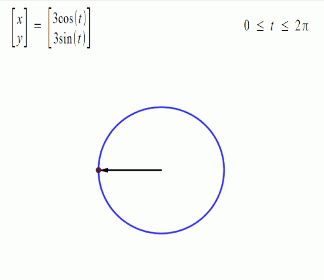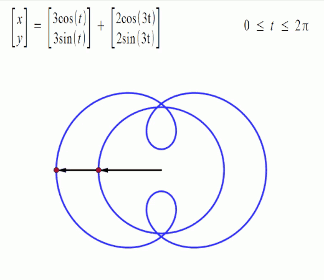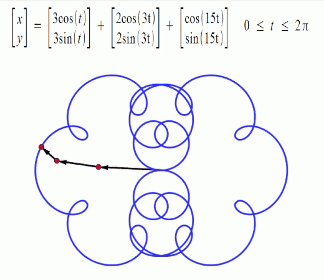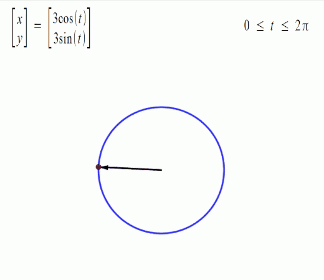
Trigonometric functions provide the easiest means of modelling the behavior of cyclical functions over time... To graph the movement patterns, one needs to have an understanding of sine and cosine functions... Using sine and cosine functions to graph a circle is a technique used in geometry called the unit circle--a circle with a radius of 1 unit…. We are then able to graph them to visualize the interactions of the different variables.” (Drexler, pp 4-11) Complex motion can be mapped in this way, including third order motion. Want to go deeper down the rabbit hole? Further detail on the Mathematics of Poi can be found HERE.
Sources:
https://84c67cd8f568acc648fb74bc321df20db70c2600.googledrive.com/host/0B3p9nx7jwyf9MjFtY3d1aXVBMjA/fourier.gif
Csikszentmihalyi, M. & Rathunde, K. (1993). The measurement of flow in everyday life: Towards a theory of emergent motivation. In Jacobs, J.E.. Developmental perspectives on motivation. Nebraska symposium on motivation. Lincoln: University of Nebraska Press.
Drexler, Ben. A Mathematical Approach to Classifying Poi Patterns. Drexfactor.com
https://docs.google.com/document/d/11DVxKtISpmnmcHcKp9wDW_ysLeKluF2iESnhm7EqF2E/edit
Woolsey. Nick. Playpoi.com













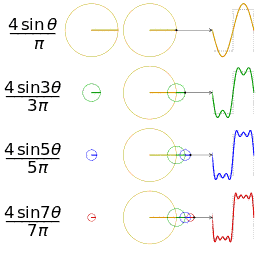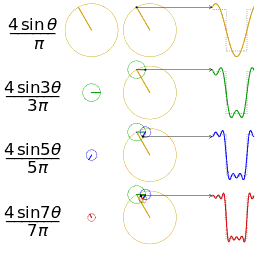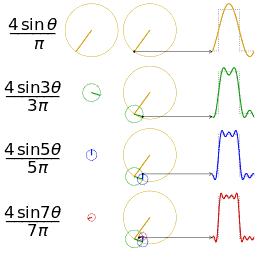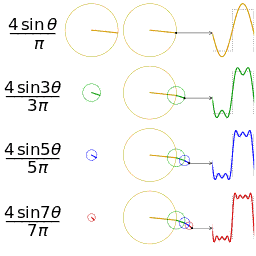
 RSS Feed
RSS Feed
